-
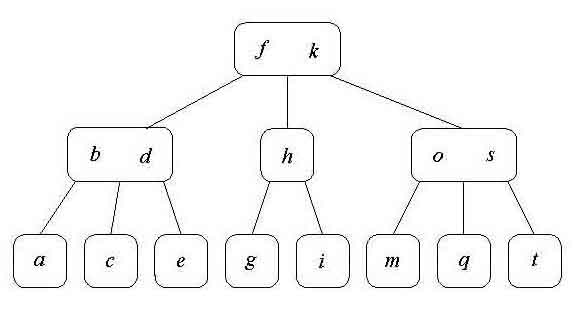
Pues eso que si alguién pilota del tema y es capaz de poder explicarme cómo llega del árbol original al de la solución se lo agradeceré. Lo que se pide es a partir del árbol B original de grado = 3 eliminar las claves 'o' e 'i' sucesivamente. Sé borrar en árboles B pero este jodío ejercicio se me resiste por 2 motivos:
1º) la sustitución que hace al eliminar la clave 'o' es por la clave 'm' en lugar de la sucesora que es lo que normalmente se haría, es decir la clave 'q'. Pienso que el motivo de esta sustitución es para evitar un caso en el que quedaría un nodo con número de claves inferior al mínimo exigido y el de su derecha e izquierda no tendrían claves suficientes (más del mínimo) para cederle una, ¿no?. 2º) ¿Se puede ceder un hijo a otro nodo que ha quedado con un número de hijos inferior al mínimo? Esto lo digo porque creo que es lo que hace cuando elimina la clave 'i'.Lo dicho si alguién sabe cómo deducirlo se lo agradecería. Por los posts que veo SATAN y vallekano quizá sepan de lo que hablo


Gracias.
-
Bueno, pues aquí me tienes, a ver si te aclaro un poco. La verdad es que me pillas con todo esto bastante olvidado y no estoy muy seguro pero te cuento como lo veo.
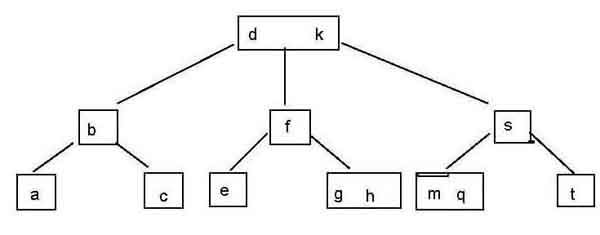
Al eliminar la clave o nos queda un nodo con un elemento y 3 hijos y eso no es permitido por lo que toca restructurar. No te se decir muy bien la sistemática pero el tema es que nos quedaría la clave S de la que cuelgan por la izquierda M y Q y por la derecha T. Pues M y Q se deben juntar en un solo nodo. Si En vez de dos claves sueltas tuviesemos subarboles habría que reestructurar estos subarboles también.
En el caso de la I…...........pues parece más lioso.
En principio eliminamos I entonces quedaría H con G por la izquierda y por la derecha nada, y eso no está permitido. No puede haber un hijo por un lado y por el otro no. Entonces yo lo que haría es subir G junto con H, formando un nodo de 2 claves. Pero si no recuerdo mal los arboles B (o eran los B+???) tienen que tener todas sus ramas con la misma profundidad (de esto no estoy muy seguro), y entonces la rama central tendría un nivel menos y por lo tanto toca reestructurar y por eso lo que hace es mover las claves de la primera rama hacia la derecha. La D sustituye a la F, la F sustituye a la H y luego se colocan las hojas y los nodos sustituidos (E, H, G).
Es algo así. De todas formas tengo en casa algoritmos de inserción en un arbol B programados en Pascal y puede que te ayuden. Eso si, te adelanto que el algoritmo de insertar es un buen tocho, que estos arbolitos tienen muuuuuuuucha miga los jodios.
Espero haberte aclarado algo, pero yo lo tengo muy olvidado. A ver si SATAN está más fresco.
-
Pues estoy igual de fresco que tu vallekano, lo he estado mirando y opino lo mismo que tu, creo que eran los B los que no pueden tener ramas de distintos niveles.
Me he puesto a hacerlo en papel y me sale como comentas tu.
La verdad es que todo esto lo tengo bastante olvidado desde que lo vi.
-
Bueno, por si te quieres volver loco he encontrado el código que decía.<br /><br />Son las funciones echas en pascal que creé para insertar elementos en un Arbol B que usaba como índice en un programa. Este arbol está implementado en un archivo en vez de en memoria.<br /><br />Ala, te pego el mazacote, haz lo que quieras con el xDxD:<br /><br /><pre>
(PROCEDIMIENTO INSERTAR CLAVE EN UN INDICE**)Procedure Insertar(x:TNombre;Var F:ArbolIndice;PosDatos:Integer);
Type
Tabla=Record
Claves:Array[1..(2k+1)] of TNombre;
Descendientes:Array[0..(2k+1)] of Integer;
Posicion:Array[1..(2*k+1)] of Integer
End;Function Vacio(B:TArbolB):Boolean;
Begin
Vacio:=(B.NumClaves=0)
End;Function ObtenerPosicion(Var F:ArbolIndice):Integer;
Begin
ObtenerPosicion:=Filesize(F)
End;Procedure InicializarNodo(Var B:TArbolB);
Var
i:Integer;
Begin
B.NumClaves:=0;
For i:=0 to 2*k do
B.Descendiente[i]:=-1
End;Procedure OrdenarLista(Var L:Tabla);
Var
i,j,DescenAux,PosFinalAux:Integer;
ClaveAux:TNombre;
Begin
ClaveAux:=L.Claves[2k+1];
DescenAux:=L.Descendientes[2k+1];
PosFinalAux:=L.Posicion[2k+1];
i:=1;
While (i<=2k+1) and (L.Claves[i]<ClaveAux) do
i:=i+1;
For j:=2*k downto i do
Begin
L.Claves[j+1]:=L.Claves[j];
L.Descendientes[j+1]:=L.Descendientes[j];
L.Posicion[j+1]:=L.Posicion[j]
End;
L.Claves[i]:=ClaveAux;
L.Descendientes[i]:=DescenAux;
L.Posicion[i]:=PosFinalAux
End;Procedure InsertarAux(Var FI:ArbolIndice;Var x:TNombre;Var NumNodo:Integer;Var Posicion:Integer;
Var Terminado,Reestructurar:Boolean;Var PosFinal:Integer);
Var
i,j,PosAux:Integer;
Lista:Tabla;
Aux,B:TArbolB;Begin
seek(FI,NumNodo);
read(FI,B);
InicializarNodo(Aux);
While not Terminado do
Begin
i:=1;
If B.Descendiente[0]=-1 then (Es una hoja)
If Vacio(B) then (Hoja Vacia)
Begin
B.Clave[1]:=x;
B.Posicion[1]:=PosFinal;
B.NumClaves:=1;
Seek(FI,NumNodo);
Write(FI,B);
Terminado:=True
End
Else
If B.NumClaves<2k then (Hoja no Vacia pero con Sitio)
Begin
While (B.Clave[i]<=x) and (i<=B.NumClaves) do
i:=i+1;
If B.Clave[i-1]=x then
Write('Clave ya existente')
Else
Begin
For j:=B.NumClaves downto i do
Begin
B.Clave[j+1]:=B.Clave[j];
B.Descendiente[j+1]:=B.Descendiente[j];
B.Posicion[j+1]:=B.Posicion[j]
End;
B.Clave[i]:=x;
B.Posicion[i]:=PosFinal;
B.NumClaves:=B.NumClaves+1;
Seek(FI,NumNodo);
Write(FI,B)
End;
Terminado:=True
End
Else (Hoja Llena)
Begin
Lista.Claves[2k+1]:=x;
Lista.Posicion[2k+1]:=PosFinal;
Posicion:=ObtenerPosicion(FI);
Lista.Descendientes[2k+1]:=Posicion;
For i:=1 to (2k) do
Lista.Claves[i]:=B.Clave[i];
For i:=1 to (2k) do
Lista.Posicion[i]:=B.Posicion[i];
For i:=0 to 2k do
Lista.Descendientes[i]:=B.Descendiente[i];
OrdenarLista(Lista);
For i:=1 to k do
B.Clave[i]:=Lista.Claves[i];
For i:=1 to k do
B.Posicion[i]:=Lista.Posicion[i];
For i:=0 to k do
B.Descendiente[i]:=Lista.Descendientes[i];
For i:=k+2 to (2k+1) do
Aux.Clave[i-k-1]:=Lista.Claves[i];
For i:=k+2 to (2k+1) do
Aux.Posicion[i-k-1]:=Lista.Posicion[i];
For i:=k+1 to (2k+1) do
Aux.Descendiente[i-k-1]:=Lista.Descendientes[i-k-1];
x:=Lista.Claves[k+1];
PosFinal:=Lista.Posicion[k+1];
B.NumClaves:=k;
Aux.NumClaves:=k;
Seek(FI,NumNodo);
Write(FI,B);
Seek(FI,Posicion);
Write(FI,Aux);
Terminado:=True;
Reestructurar:=True
EndElse (*El nodo no es una hoja*) Begin While (B.Clave[i]<=x) and (i<=B.NumClaves) do i:=i+1; If B.Clave[i-1]=x then Write('Clave ya existente') Else Begin InsertarAux(FI,x,B.Descendiente[i-1],Posicion,Terminado,Reestructurar,PosFinal); If Reestructurar then (*Nodo Intermedio a reestructurar*) If B.NumClaves<2*k then Begin While (B.Clave[i]<=x) and (i<=B.NumClaves) do i:=i+1; If B.Clave[i-1]=x then Write('Clave ya existente') Else Begin For j:=B.NumClaves downto i do Begin B.Clave[j+1]:=B.Clave[j]; B.Posicion[j+1]:=B.Posicion[j]; B.Descendiente[j+1]:=B.Descendiente[j] End; B.Clave[i]:=x; B.Posicion[i]:=PosFinal; B.Descendiente[i]:=Posicion; B.NumClaves:=B.NumClaves+1; Seek(FI,NumNodo); Write(FI,B) End; Terminado:=True; Reestructurar:=False End Else (*Nodo intermedio a reestructurar sin sitio*) Begin Lista.Claves[2*k+1]:=x; Lista.Posicion[2*k+1]:=PosFinal; PosAux:=ObtenerPosicion(FI); Lista.Descendientes[2*k+1]:=Posicion; For i:=1 to (2*k) do Lista.Claves[i]:=B.Clave[i]; For i:=1 to (2*k) do Lista.Posicion[i]:=B.Posicion[i]; For i:=0 to 2*k do Lista.Descendientes[i]:=B.Descendiente[i]; OrdenarLista(Lista); For i:=1 to k do B.Clave[i]:=Lista.Claves[i]; For i:=1 to k do B.Posicion[i]:=Lista.Posicion[i]; For i:=0 to k do B.Descendiente[i]:=Lista.Descendientes[i]; For i:=k+2 to (2*k+1) do Aux.Clave[i-k-1]:=Lista.Claves[i]; For i:=k+2 to (2*k+1) do Aux.Posicion[i-k-1]:=Lista.Posicion[i]; For i:=k+1 to (2*k+1) do Aux.Descendiente[i-k-1]:=Lista.Descendientes[i]; x:=Lista.Claves[k+1]; PosFinal:=Lista.Posicion[k+1]; B.NumClaves:=k; Aux.NumClaves:=k; Seek(FI,NumNodo); Write(FI,B); Seek(FI,PosAux); Write(FI,Aux); Posicion:=PosAux; Terminado:=True; Reestructurar:=True End End End EndEnd;
Var
Raiz,aux:TArbolB;
Posicion,Pos,i:Integer;
Terminado,Reestructurar:Boolean;Begin
seek(F,0);
read(F,Raiz);
Terminado:=False;
Reestructurar:=False;
InsertarAux(F,x,Raiz.Descendiente[0],Posicion,Terminado,Reestructurar,PosDatos);
If Reestructurar then
Begin
InicializarNodo(aux);
aux.Clave[1]:=x;
aux.Posicion[1]:=PosDatos;
aux.Descendiente[0]:=Raiz.Descendiente[0];
aux.Descendiente[1]:=Posicion;
aux.NumClaves:=1;
Pos:=ObtenerPosicion(F);
Seek(F,Pos);
Write(F,Aux);
Raiz.Descendiente[0]:=Pos;
Seek(F,0);
Write(F,Raiz)
End
End;
(****FIN INSERTAR CLAVE EN INDICE)
[/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i]</pre> -
Muchas gracias a los 2. Efectivamente son los B los que tienen que tener todas las hojas al mismo nivel. El problema lo tengo en el borrado de la 'i'. Efectivamente al borrar la 'i' ese nodo queda con menos claves del mínimo (1 en este caso) pues pasa a tener 0 claves. Consideramos el nodo que está a su izquierda y a su derecha (que tienen el mismo padre que él) y vemos si alguno tiene más claves del mínimo exigido. No tiene nodo derecho y el izquierdo tiene una sola clave, 'g' así que lo que hacemos es fusionar en el nodo que contiene a 'g' a ésta con la 'h' del nodo padre. Ahora el nodo padre (el que contenía 'h') es el que queda con menos claves (0 en este caso) que el mínimo exigido (1). Así que de nuevo nodo izdo. y derecho. En este caso el izdo. tiene 2 claves así que le pasa una a su nodo padre (la 'd') y éste al nodo que ha quedado con 0 claves le pasa una tb (la 'f'). El problema viene ahora pues el nodo padre 'f' queda con un solo hijo y como mínimo ha de tener 2. Lo que creo que hace es pasarle un nodo, el siguiente en orden de claves, para completar su número de nodos hasta 2. Esto lo supongo pk en mis apuntes desde luego ese caso no se contempla ni nada por el estilo. Además por más que he buscado documentación no aparece nada referente a cesión de hijos por parte de un nodo a otro y eso es lo que me desconcertaba. :rabieta: :rabieta:
En fin que muchas gracias y si sabéis de algún sitio o documento en el que se contemple este caso os agradeceré me lo comuniquéis. ;DP.D. vallekano gracias por el código en Pascal o mejor dixo por el proyectil ;D
-
Pues como links no te puedo recomendar nada ahora mismo porque no tengo mi ordenador con los favoritos aqui, pero te recomiendo como buen libro de estructuras de datos el del autor del pascal, es decir nicklaus wirth (creo que se pone asi), creo que el libro se llama "estructuras de datos", esta muy bien, yo lo tengo en mis compras pendientes.
-
<small>@vallekano:</small><br><blockquote>Bueno, por si te quieres volver loco he encontrado el código que decía.<br /><br />Son las funciones echas en pascal que creé para insertar elementos en un Arbol B que usaba como índice en un programa. Este arbol está implementado en un archivo en vez de en memoria.<br /><br />Ala, te pego el mazacote, haz lo que quieras con el xDxD:<br /><br /><pre>
(PROCEDIMIENTO INSERTAR CLAVE EN UN INDICE**)Procedure Insertar(x:TNombre;Var F:ArbolIndice;PosDatos:Integer);
Type
Tabla=Record
Claves:Array[1..(2k+1)] of TNombre;
Descendientes:Array[0..(2k+1)] of Integer;
Posicion:Array[1..(2*k+1)] of Integer
End;Function Vacio(B:TArbolB):Boolean;
Begin
Vacio:=(B.NumClaves=0)
End;Function ObtenerPosicion(Var F:ArbolIndice):Integer;
Begin
ObtenerPosicion:=Filesize(F)
End;Procedure InicializarNodo(Var B:TArbolB);
Var
i:Integer;
Begin
B.NumClaves:=0;
For i:=0 to 2*k do
B.Descendiente[i]:=-1
End;Procedure OrdenarLista(Var L:Tabla);
Var
i,j,DescenAux,PosFinalAux:Integer;
ClaveAux:TNombre;
Begin
ClaveAux:=L.Claves[2k+1];
DescenAux:=L.Descendientes[2k+1];
PosFinalAux:=L.Posicion[2k+1];
i:=1;
While (i<=2k+1) and (L.Claves[i]<ClaveAux) do
i:=i+1;
For j:=2*k downto i do
Begin
L.Claves[j+1]:=L.Claves[j];
L.Descendientes[j+1]:=L.Descendientes[j];
L.Posicion[j+1]:=L.Posicion[j]
End;
L.Claves[i]:=ClaveAux;
L.Descendientes[i]:=DescenAux;
L.Posicion[i]:=PosFinalAux
End;Procedure InsertarAux(Var FI:ArbolIndice;Var x:TNombre;Var NumNodo:Integer;Var Posicion:Integer;
Var Terminado,Reestructurar:Boolean;Var PosFinal:Integer);
Var
i,j,PosAux:Integer;
Lista:Tabla;
Aux,B:TArbolB;Begin
seek(FI,NumNodo);
read(FI,B);
InicializarNodo(Aux);
While not Terminado do
Begin
i:=1;
If B.Descendiente[0]=-1 then (Es una hoja)
If Vacio(B) then (Hoja Vacia)
Begin
B.Clave[1]:=x;
B.Posicion[1]:=PosFinal;
B.NumClaves:=1;
Seek(FI,NumNodo);
Write(FI,B);
Terminado:=True
End
Else
If B.NumClaves<2k then (Hoja no Vacia pero con Sitio)
Begin
While (B.Clave[i]<=x) and (i<=B.NumClaves) do
i:=i+1;
If B.Clave[i-1]=x then
Write('Clave ya existente')
Else
Begin
For j:=B.NumClaves downto i do
Begin
B.Clave[j+1]:=B.Clave[j];
B.Descendiente[j+1]:=B.Descendiente[j];
B.Posicion[j+1]:=B.Posicion[j]
End;
B.Clave[i]:=x;
B.Posicion[i]:=PosFinal;
B.NumClaves:=B.NumClaves+1;
Seek(FI,NumNodo);
Write(FI,B)
End;
Terminado:=True
End
Else (Hoja Llena)
Begin
Lista.Claves[2k+1]:=x;
Lista.Posicion[2k+1]:=PosFinal;
Posicion:=ObtenerPosicion(FI);
Lista.Descendientes[2k+1]:=Posicion;
For i:=1 to (2k) do
Lista.Claves[i]:=B.Clave[i];
For i:=1 to (2k) do
Lista.Posicion[i]:=B.Posicion[i];
For i:=0 to 2k do
Lista.Descendientes[i]:=B.Descendiente[i];
OrdenarLista(Lista);
For i:=1 to k do
B.Clave[i]:=Lista.Claves[i];
For i:=1 to k do
B.Posicion[i]:=Lista.Posicion[i];
For i:=0 to k do
B.Descendiente[i]:=Lista.Descendientes[i];
For i:=k+2 to (2k+1) do
Aux.Clave[i-k-1]:=Lista.Claves[i];
For i:=k+2 to (2k+1) do
Aux.Posicion[i-k-1]:=Lista.Posicion[i];
For i:=k+1 to (2k+1) do
Aux.Descendiente[i-k-1]:=Lista.Descendientes[i-k-1];
x:=Lista.Claves[k+1];
PosFinal:=Lista.Posicion[k+1];
B.NumClaves:=k;
Aux.NumClaves:=k;
Seek(FI,NumNodo);
Write(FI,B);
Seek(FI,Posicion);
Write(FI,Aux);
Terminado:=True;
Reestructurar:=True
EndElse (*El nodo no es una hoja*) Begin While (B.Clave[i]<=x) and (i<=B.NumClaves) do i:=i+1; If B.Clave[i-1]=x then Write('Clave ya existente') Else Begin InsertarAux(FI,x,B.Descendiente[i-1],Posicion,Terminado,Reestructurar,PosFinal); If Reestructurar then (*Nodo Intermedio a reestructurar*) If B.NumClaves<2*k then Begin While (B.Clave[i]<=x) and (i<=B.NumClaves) do i:=i+1; If B.Clave[i-1]=x then Write('Clave ya existente') Else Begin For j:=B.NumClaves downto i do Begin B.Clave[j+1]:=B.Clave[j]; B.Posicion[j+1]:=B.Posicion[j]; B.Descendiente[j+1]:=B.Descendiente[j] End; B.Clave[i]:=x; B.Posicion[i]:=PosFinal; B.Descendiente[i]:=Posicion; B.NumClaves:=B.NumClaves+1; Seek(FI,NumNodo); Write(FI,B) End; Terminado:=True; Reestructurar:=False End Else (*Nodo intermedio a reestructurar sin sitio*) Begin Lista.Claves[2*k+1]:=x; Lista.Posicion[2*k+1]:=PosFinal; PosAux:=ObtenerPosicion(FI); Lista.Descendientes[2*k+1]:=Posicion; For i:=1 to (2*k) do Lista.Claves[i]:=B.Clave[i]; For i:=1 to (2*k) do Lista.Posicion[i]:=B.Posicion[i]; For i:=0 to 2*k do Lista.Descendientes[i]:=B.Descendiente[i]; OrdenarLista(Lista); For i:=1 to k do B.Clave[i]:=Lista.Claves[i]; For i:=1 to k do B.Posicion[i]:=Lista.Posicion[i]; For i:=0 to k do B.Descendiente[i]:=Lista.Descendientes[i]; For i:=k+2 to (2*k+1) do Aux.Clave[i-k-1]:=Lista.Claves[i]; For i:=k+2 to (2*k+1) do Aux.Posicion[i-k-1]:=Lista.Posicion[i]; For i:=k+1 to (2*k+1) do Aux.Descendiente[i-k-1]:=Lista.Descendientes[i]; x:=Lista.Claves[k+1]; PosFinal:=Lista.Posicion[k+1]; B.NumClaves:=k; Aux.NumClaves:=k; Seek(FI,NumNodo); Write(FI,B); Seek(FI,PosAux); Write(FI,Aux); Posicion:=PosAux; Terminado:=True; Reestructurar:=True End End End EndEnd;
Var
Raiz,aux:TArbolB;
Posicion,Pos,i:Integer;
Terminado,Reestructurar:Boolean;Begin
seek(F,0);
read(F,Raiz);
Terminado:=False;
Reestructurar:=False;
InsertarAux(F,x,Raiz.Descendiente[0],Posicion,Terminado,Reestructurar,PosDatos);
If Reestructurar then
Begin
InicializarNodo(aux);
aux.Clave[1]:=x;
aux.Posicion[1]:=PosDatos;
aux.Descendiente[0]:=Raiz.Descendiente[0];
aux.Descendiente[1]:=Posicion;
aux.NumClaves:=1;
Pos:=ObtenerPosicion(F);
Seek(F,Pos);
Write(F,Aux);
Raiz.Descendiente[0]:=Pos;
Seek(F,0);
Write(F,Raiz)
End
End;
(****FIN INSERTAR CLAVE EN INDICE)No tendrias tambien el de Insertar?
Yo trato de modificar el de memoria principal a fichero y no hay manera...[/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i][/i]</pre></blockquote> -
Puffff, pues debería. Esta noche si me acuerdo te lo busco.
EDITO: El de insertar es el que te pegué no??? Ahora, no se como estará programado. Era de los primeros programas que hacía, hace muchos años.
-
Perdón, fallo mio, me referia al de "borrado".
Entiendo que es el proceso inverso (+ ó -) pero por más que me ayudo del de borrado en memoria y del de insertar tuyo no entiendo porque me falla, será alguna chorrada pero me esta volviendo tarumba y si eso era por comparar…