@Twikzer:
De echo un 4770K que es un quadcore a 3.5Ghz es más rápido en 32M
una cosa que no entiendo, me puse a probar con el wprime, y si le pongo 12 threds, me sale mejor seultado en el de 32M que si le pongo 16, por que? si le pongo 8 sale un poco pero que si le pongo 16, pero solo 0.100 aprox
Ya te lo he contestado antes  … tu OC está mal echo y para colmo seguramente no es suficientemente estable... pasa con Wprime, con CINEBENCH y con muchos benchmarks... es señal de una mala configuración en Bios o de que el OC es poco estable.
… tu OC está mal echo y para colmo seguramente no es suficientemente estable... pasa con Wprime, con CINEBENCH y con muchos benchmarks... es señal de una mala configuración en Bios o de que el OC es poco estable.
En tu caso puede ser que al reducir el numero de hilos de ejecución el CPU se calienta menos y por tanto el OC se resiente menos pero vamos que es tan facil como pasar Prime95, OCCT o el LinX
Personalmente recomiendo LinX pero simpre es mejor empezar con Prime95…OCCT lo bueno es que tiene monitorización de parametros y registra el comportamiento durante el stress test pero el LINPACK que trae no está actualizado a la ultima versión por lo que no exprime Haswell ni Skylake al máximo… una pena porque es un programa muy bueno pero que no se está actualizando. :llorar:
Por resumir... BENCHMARKS CON RESULTADO RARO-> OC MAL HECHO O INESTABLE ;D
Si te pierdes con el tema estabilidad mirate estas guias:
**
**
EDITO
ojo.. no se pueden comparar dos versiones distintas:
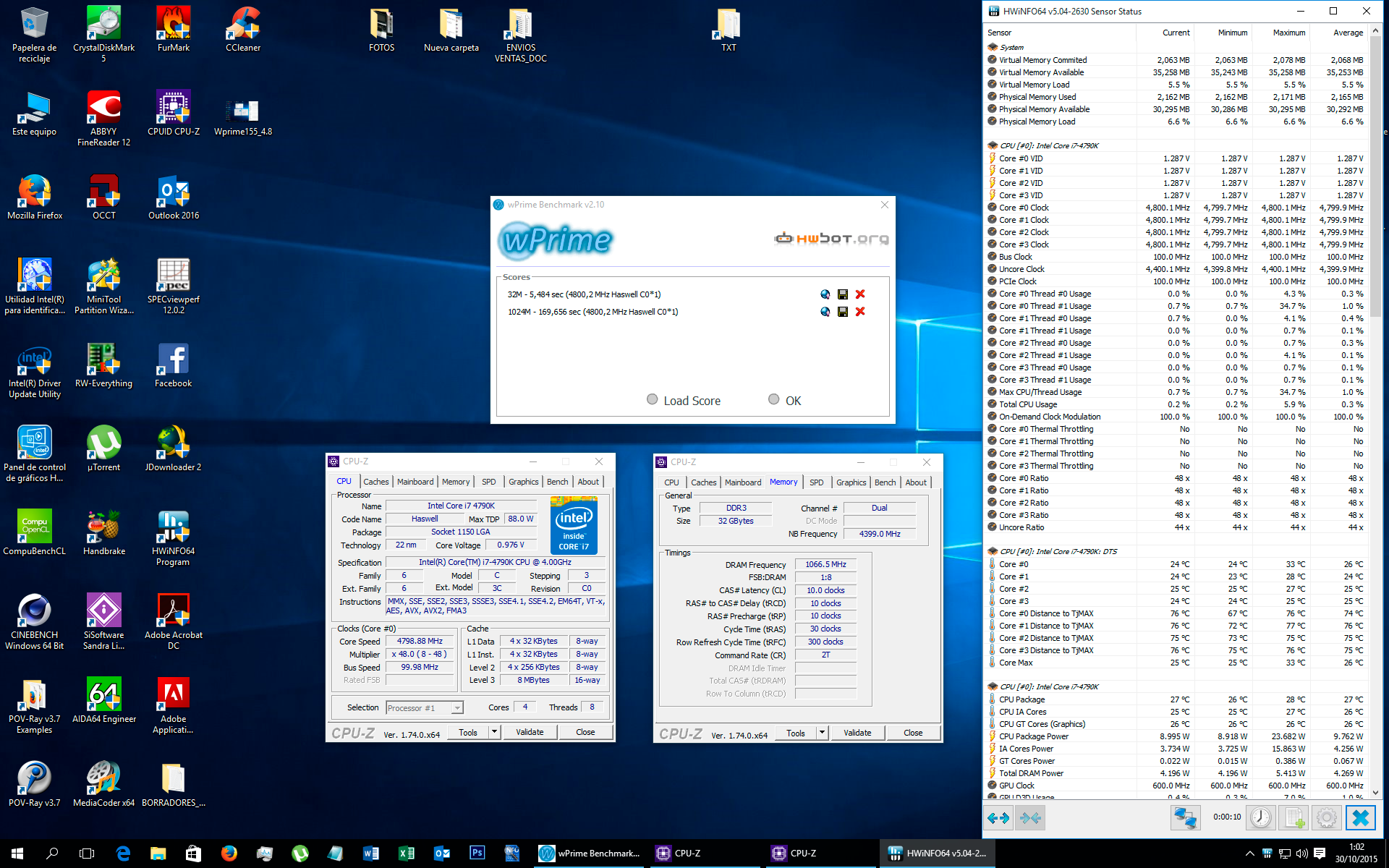
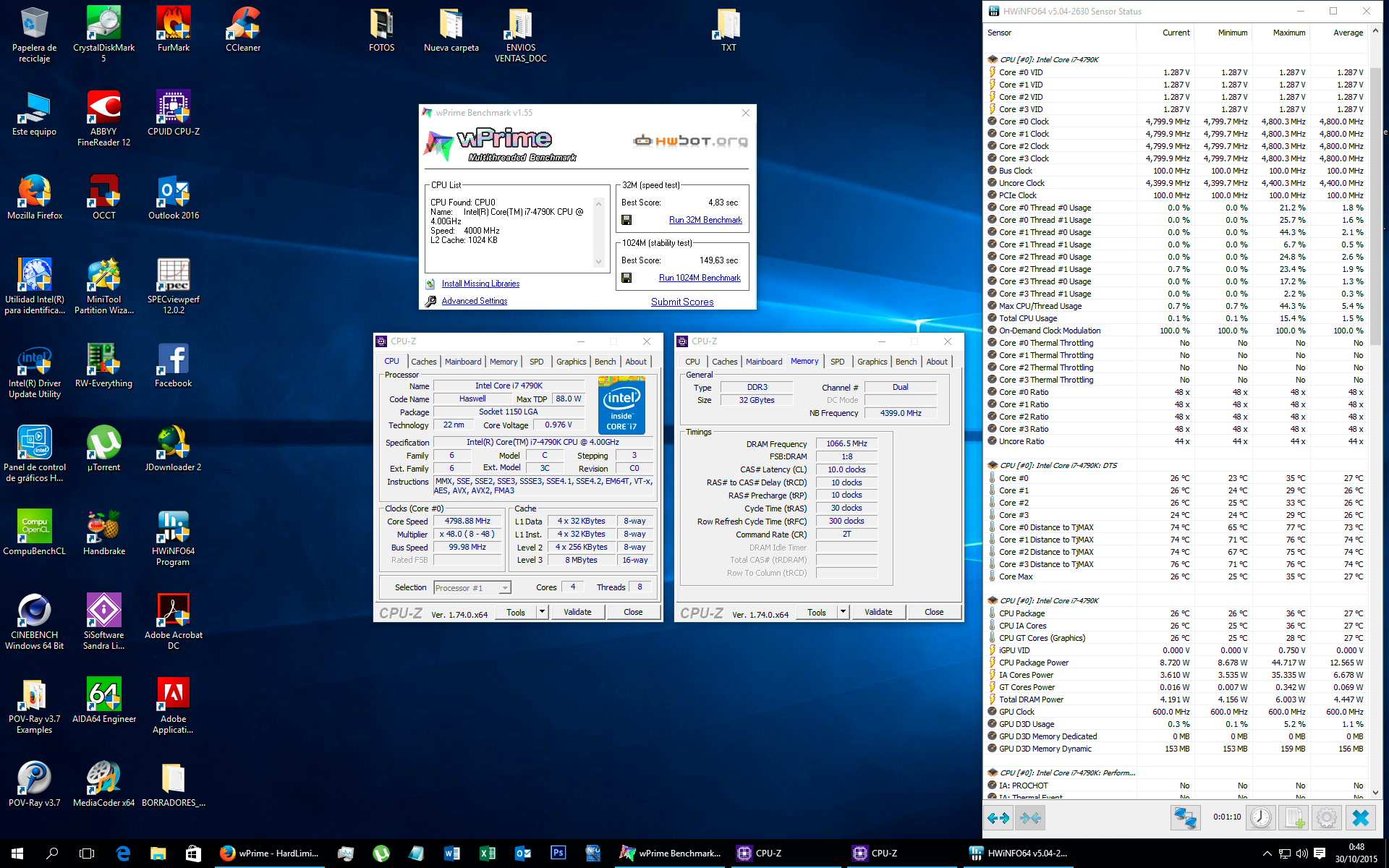
Pese a ello tus resultados son anómalos.